Demo Parameters Estimation

This is an advanced tutorial. Be sure to get through Demo Train, Demo Dense and read Section 2.6 of the PhD Thesis Multi-Layer Conditional Random Fields for Revealing Unobserved Entities before proceeding with this tutorial.

In many practical applications, CRFs have lack of expressivity and a groundtruth label map may not be the solution of the CRF model. In order to handle this problem and get more control over the classification process with CRFs, we may introduce additional control parameters training.

As a base for this tutorial we take the code from Demo Dense. The model control parameters there are the numerical arguments to the functions DirectGraphicalModels::CGraphExt::addDefaultEdgesModel(), namely the value specifying the smoothness strength and the weighting parameter. In total Demo Dense code includes 4 control parameters, which were selected empirically. In this tutorial we will try to select these parameters automatically in such a way that they will be optimal it terms of the classification accuracy.

Init Parameters		Resulting Parameters
{ 100, 300, 3, 10 }		{ 90, 310, 29.5, 7.9 }
Class Map with accuracy 87.31 %		Class Map with accuracy 90.07 %

In contrast to the internal parameters of the potential functions, model control parameters are estimated separately, after the potentials are trained. This results in an additional second training phase. We start with gathering all the parameters into one vector vParams. We initialize the values of this vector with those values from the original Demo Dense code. The order of the parameters is important: they will be optimized in the same order as they met in the vector vParams. So, we put first two values specifying the smoothness strength of both edge models and then the corresponding weighting parameters.

const std::vector<float> vInitParams = { 100.0f, 300.0f, 3.0f, 10.0f };
const std::vector<float> vInitDeltas = { 10.0f, 10.0f, 1.0f, 1.0f };
      std::vector<float> vParams     = vInitParams;                         // Actual model parameters

Then we initialize the Powell search class. The vector vInitDeltas containes the minimal step values for the search algorithm to change the parameters. The order of these values corresponds to the order of parameters in vInitParams. Too small values in vInitDeltas may make the search more accurate, but also more slow and increase the probability of stucking in a local extremum. Too large values may lead to oscillation and poor convergence.

using namespace DirectGraphicalModels;

CPowell powell(vParams.size());
powell.setInitParams(vInitParams);
powell.setDeltas(vInitDeltas);

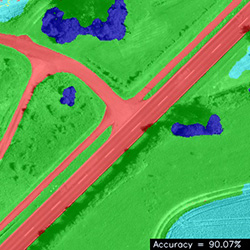
The parameters are optimized in the mail loop where we gather graph filling, decoding and evaluation phases with the help of DirectGraphicalModels::CPowell::getParams(). This function takes as argument one floating-point number and returns a vector, containing new parameters which should lead to increase of the argument. In this tutorial we use the overall classification accuracy as the measure to maximize. However it might be a weighted sum of per-class accuracies (i.e. sum of the diagonal elements of the confusion matrix).

// ========================= Training Node Potentials=========================
nodeTrainer->addFeatureVecs(train_fv, train_gt);
nodeTrainer->train();

// Main loop of parameters optimization
for (int i = 1; ; i++) {
    // ================= Filling the Graph =====================
    Mat nodePotentials = nodeTrainer->getNodePotentials(test_fv);               // Classification: CV_32FC(nStates) <- CV_8UC(nFeatures)
    graphKit->getGraphExt().setGraph(nodePotentials);                           // Filling-in the graph nodes
    graphKit->getGraphExt().addDefaultEdgesModel(vParams[0], vParams[2]);
    graphKit->getGraphExt().addDefaultEdgesModel(test_fv, vParams[1], vParams[3]);

    // ====================== Decoding =========================
    vec_byte_t optimalDecoding = graphKit->getInfer().decode(100);

    // ====================== Evaluation =======================
    Mat solution(imgSize, CV_8UC1, optimalDecoding.data());
    confMat.estimate(test_gt, solution);
    
    printf("Iteration: %d, parameters: { ", i);
    for (const float& param : vParams) printf("%.1f ", param);
    printf("}, accuracy: %.2f%%\n", confMat.getAccuracy());

    if (powell.isConverged()) break;
    vParams = powell.getParams(confMat.getAccuracy());
    graphKit->getGraph().reset();
    confMat.reset();
}

vParams = powell.getParams(1);
printf("Resulting parameters: {");
for (const float& param : vParams) printf("%.1f ", param);
printf("}\n");

Please note, that we have to reset both the graph and the confusion matrix after each iteration in the main loop.