 |
Direct Graphical Models
v.1.7.0
|
 |
Direct Graphical Models
v.1.7.0
|
Multivariate Gaussian distribution class. More...
#include <KDGauss.h>
Public Member Functions | |
| CKDGauss (dword k) | |
| Constructor. More... | |
| CKDGauss (const Mat &mu) | |
| Constructor. More... | |
| CKDGauss (const CKDGauss &rhs) | |
| Copy constructor. More... | |
| CKDGauss & | operator= (const CKDGauss &rhs) |
| Copy operator. More... | |
| CKDGauss & | operator+= (const CKDGauss &rhs) |
| Compound merge operator. More... | |
| CKDGauss & | operator+= (const Mat &point) |
| Compound merge operator. More... | |
| void | clear (void) |
| Clears class variables. More... | |
| bool | empty (void) const |
| Checks weather the Gaussian function is approximated. More... | |
Accessors | |
| void | setNumPoints (long nPoints) |
| Sets the number of approximation points. More... | |
| size_t | getNumPoints (void) const |
| Returns the number of approximation points. More... | |
| void | setMu (Mat &mu) |
| Sets \(\mu\). More... | |
| Mat | getMu (void) const |
| Returns \(\mu\). More... | |
| void | setSigma (Mat &sigma) |
| Sets \(\Sigma\). More... | |
| Mat | getSigma (void) const |
| Returns \(\Sigma\). More... | |
Main functionality | |
| void | addPoint (const Mat &point, bool approximate=false) |
| Adds new k-dimensional point (sample) for Gaussian distribution approximation. More... | |
| long double | getAlpha (void) const |
| Returns \(\alpha\). More... | |
| double | getValue (Mat &x, Mat &aux1=EmptyMat, Mat &aux2=EmptyMat, Mat &aux3=EmptyMat) const |
| Returns unscaled value of the Gaussian function. More... | |
| Mat | getSample (void) const |
| Returns a random vector (sample) from multivariate normal distribution. More... | |
Similarity measures | |
| double | getEuclidianDistance (const Mat &x) const |
| Returns the Euclidian distance between argument point x and the center of multivariate normal distribution \(\mu\). More... | |
| double | getMahalanobisDistance (const Mat &x) const |
| Returns the Mahalanobis distance between argument point x and the center of multivariate normal distribution \(\mathcal{N}(\mu,\Sigma)\). More... | |
| double | getKullbackLeiberDivergence (const CKDGauss &x) const |
| Returns the Kullback-Leiber divergence from the multivariate normal distribution \(\mathcal{N}(\mu,\Sigma)\) to argument multivariate normal distribution \(\mathcal{N}_x(\mu_x,\Sigma_x)\). More... | |
Private Member Functions | |
| Mat | getSigmaInv (void) const |
| Returns \(\Sigma^{-1}\). More... | |
| void | reset_SigmaInv_Q_Alpha (void) |
| Mat | calculateQ (void) const |
Private Attributes | |
| size_t | m_nPoints |
| Mat | m_mu |
| Mat | m_sigma |
| Mat | m_sigmaInv = Mat() |
| Mat | m_Q = Mat() |
| long double | m_alpha = -1 |
Static Private Attributes | |
| static const bool | USE_SAFE_SIGMA = false |
Multivariate Gaussian distribution class.
This class allows to approximate the distribution of random variables (samples) \( \textbf{x} \), represented as k - dinemstional points \( [x_1,x_2,\dots,x_k] \). Under the assumption, that the random variables \( \textbf{x} \) are normally distributed, the approximation is done with multivariate normal distribution:
\[ \mathcal{N}_k(\mu,\Sigma)= \alpha\cdot\exp\big( -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\big), \]
whith coefficient \( \alpha = \frac{1}{(2\pi)^{k/2}|\Sigma|^{1/2}} \). The parameters \( \mu\) and \(\Sigma \) of the Gaussian function \( \mathcal{N}(\mu,\Sigma) \) may be estimated sequentially with function addPoint() or operator operator+=(const Mat &); also they may be set directly with functions setMu() and setSigma().
The value of the Gaussian function \( \mathcal{N}(\mu,\Sigma) \) in point \( \textbf{x} \) is achieved with the functions getAlpha() and getValue():
In order to generate a random sample from the distribution, given by Gaussian function \( \mathcal{N}(\mu,\Sigma) \), one uses function getSample().
| DirectGraphicalModels::CKDGauss::CKDGauss | ( | dword | k | ) |
| DirectGraphicalModels::CKDGauss::CKDGauss | ( | const Mat & | mu | ) |
Constructor.
The dimension of the Gauss function will be derived from the dimension k of the argument \(\mu\)
| mu | The mean vector \(\mu\) : Mat(size: k x 1; type: CV_XXC1) |
Definition at line 19 of file KDGauss.cpp.
| DirectGraphicalModels::CKDGauss::CKDGauss | ( | const CKDGauss & | rhs | ) |
Copy constructor.
Definition at line 27 of file KDGauss.cpp.
| void DirectGraphicalModels::CKDGauss::addPoint | ( | const Mat & | point, |
| bool | approximate = false |
||
| ) |
Adds new k-dimensional point (sample) for Gaussian distribution approximation.
This function is an analog to the merging operator (Ref. operator+=()) and updates the Gaussian distribution in respect to one new observed point, using the following update rules:
\[ \begin{aligned} \hat{\mu} &= \frac{n\mu + p}{n + 1} \\ \hat{\Sigma} &= \frac{n(\Sigma + \mu\mu^\top) + p~p^\top}{n + 1} - \hat{\mu}\hat{\mu}^\top \\ \end{aligned} \]
| point | k-dimensional point: Mat(size: k x 1; type: CV_64FC1) |
| approximate | Flag indicating whether a faster approximation of the update rule for \(\Sigma\) should be used: \( \hat{\Sigma} = \frac{n\Sigma + (p-\hat{\mu})(p-\hat{\mu})^\top}{n + 1} \). For large \(n\) this approximation is equevalent to the original update rool. |
Definition at line 90 of file KDGauss.cpp.


|
private |
| void DirectGraphicalModels::CKDGauss::clear | ( | void | ) |
Clears class variables.
Allows to re-use the class
Definition at line 81 of file KDGauss.cpp.

|
inline |
| long double DirectGraphicalModels::CKDGauss::getAlpha | ( | void | ) | const |
Returns \(\alpha\).
Definition at line 163 of file KDGauss.cpp.
| double DirectGraphicalModels::CKDGauss::getEuclidianDistance | ( | const Mat & | x | ) | const |
Returns the Euclidian distance between argument point x and the center of multivariate normal distribution \(\mu\).
The Euclidian distance is calculated by the formula: \(D_E(\mathcal{N};x)=\sqrt{ (x-\mu)^\top(x-\mu) }\).
| x | A k-dimensional point (sample): Mat(size: k x 1; type: CV_64FC1) |
Definition at line 189 of file KDGauss.cpp.
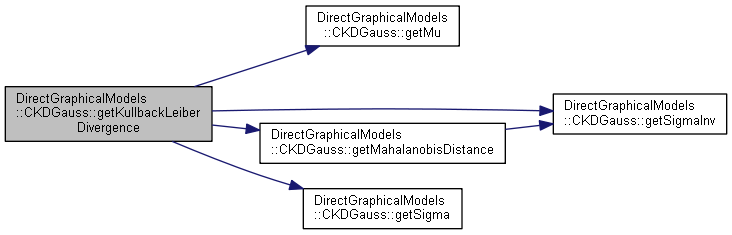
| double DirectGraphicalModels::CKDGauss::getKullbackLeiberDivergence | ( | const CKDGauss & | x | ) | const |
Returns the Kullback-Leiber divergence from the multivariate normal distribution \(\mathcal{N}(\mu,\Sigma)\) to argument multivariate normal distribution \(\mathcal{N}_x(\mu_x,\Sigma_x)\).
The Kullback-Leiber divergence (or relative entropy) is calculated by the formula: \(D_{KL}(\mathcal{N};\mathcal{N}_x)=\frac{1}{2}\Big( tr(\Sigma^{-1}_{x}\Sigma) + D^{2}_{M}(\mathcal{N}_x;\mu) - k - \ln\big(\frac{\left|\Sigma\right|}{\left|\Sigma_x\right|}\big) \Big)\) and expressed in nats. Here \(D_M(\mathcal{N}_x;\mu)\) is the Mahalanobis distance beween the centers of multivariate normal distributions \(\mu_x\) and \(\mu\) with respect to \(\mathcal{N}_x\) (see getMahalanobisDistance() for more details). Please note, that it is not a symmetrical quantity, that is to say \( D_{KL}(\mathcal{N};\mathcal{N}_x) \neq D_{KL}(\mathcal{N}_x;\mathcal{N})\) and so could be hardly used as a "distance".
| x | multivariate normal distribution \(\mathcal{N}_x(\mu_x,\Sigma_x)\) of the dimension k. |
Definition at line 207 of file KDGauss.cpp.
| double DirectGraphicalModels::CKDGauss::getMahalanobisDistance | ( | const Mat & | x | ) | const |
Returns the Mahalanobis distance between argument point x and the center of multivariate normal distribution \(\mathcal{N}(\mu,\Sigma)\).
The Mahalanobis distance is calculated by the formula: \(D_M(\mathcal{N};x)=\sqrt{ (x-\mu)^\top\Sigma^{-1}(x-\mu) }\)
| x | n-dimensional point (sample): Mat(size: k x 1; type: CV_64FC1) |
Definition at line 198 of file KDGauss.cpp.


|
inline |
|
inline |
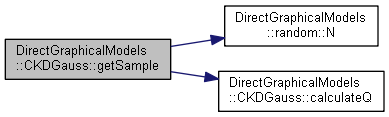
| Mat DirectGraphicalModels::CKDGauss::getSample | ( | void | ) | const |
Returns a random vector (sample) from multivariate normal distribution.
The implementation is based on the paper Generating Random Vectors from the Multivariate Normal Distribution
Definition at line 229 of file KDGauss.cpp.
|
inline |
|
private |
Returns \(\Sigma^{-1}\).
Definition at line 156 of file KDGauss.cpp.

| double DirectGraphicalModels::CKDGauss::getValue | ( | Mat & | x, |
| Mat & | aux1 = EmptyMat, |
||
| Mat & | aux2 = EmptyMat, |
||
| Mat & | aux3 = EmptyMat |
||
| ) | const |
Returns unscaled value of the Gaussian function.
This function returns unscaled value of the Gaussian function, i.e. \( \exp\big( -\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)\big) \). In order to get the value of \( \mathcal{N}_k(\mu,\Sigma) \), the output of this function must be multiplied with \( \alpha \) from the getAlpha() function.
This function is PPL-safe function.
| x | n-dimensional point (sample): Mat(size: k x 1; type: CV_64FC1) |
| aux1 | Auxilary variable |
| aux2 | Auxilary variable |
| aux3 | Auxilary variable |
Definition at line 175 of file KDGauss.cpp.

Compound merge operator.
This operator merges two Gaussian distributions together:
\[ \begin{aligned} \hat{\mu} &= \frac{n_1\mu_1 + n_2\mu_2}{n1 + n2} \\ \hat{\Sigma} &= \frac{n_1(\Sigma_1 + \mu_1\mu^{\top}_{1}) + n2(\Sigma_2 + \mu_2\mu^{\top}_{2})}{n_1 + n_2} - \hat{\mu}\hat{\mu}^\top \\ \end{aligned} \]
For the sequential Gauss function estimation one also may use this operator (see the code below) or addPoint() function:
In this case \(n_2 = 1\) and \(\Sigma_2 = 0\).
Definition at line 50 of file KDGauss.cpp.

| CKDGauss & DirectGraphicalModels::CKDGauss::operator+= | ( | const Mat & | point | ) |
Compound merge operator.
This operator is equivalent to
and might be used for sequential estimation of the Gaussian distribution
Definition at line 75 of file KDGauss.cpp.

Copy operator.
Definition at line 37 of file KDGauss.cpp.
|
inlineprivate |
| void DirectGraphicalModels::CKDGauss::setMu | ( | Mat & | mu | ) |
Sets \(\mu\).
| mu | the mean vector \(\mu\) : Mat(size: k x 1; type: CV_64FC1) |
Definition at line 134 of file KDGauss.cpp.

|
inline |
| void DirectGraphicalModels::CKDGauss::setSigma | ( | Mat & | sigma | ) |
Sets \(\Sigma\).
| sigma | the covariance matrix \(\Sigma\): Diagonal Mat(size: k x k; type: CV_64FC1) |
Definition at line 145 of file KDGauss.cpp.

|
mutableprivate |
|
mutableprivate |
|
mutableprivate |
|
staticprivate |