Training Statistical Models
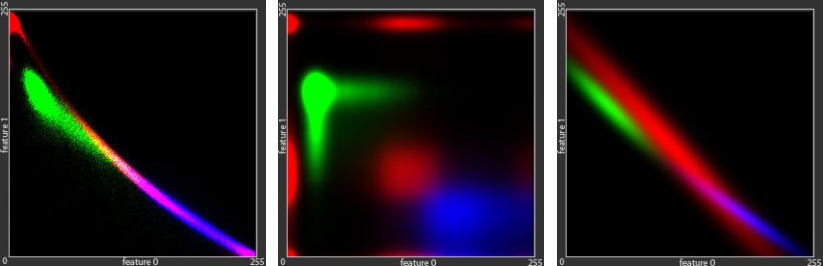
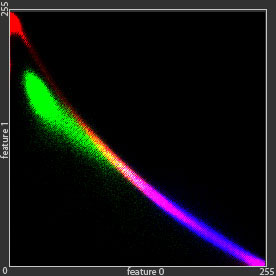
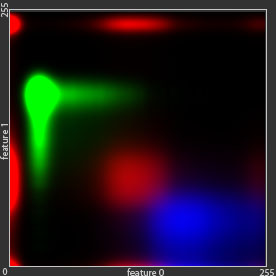
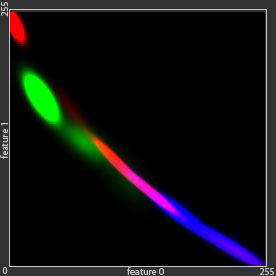
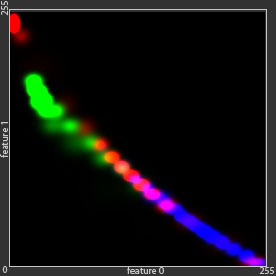
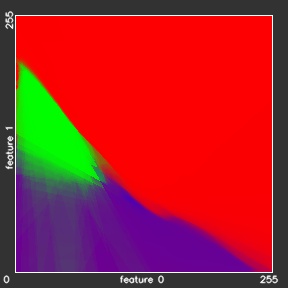
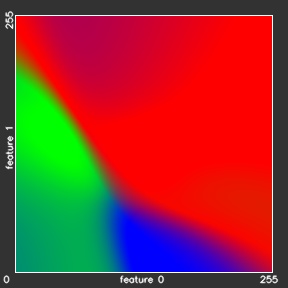
There is a wide variety of statistical models which may be applied to the semantic segmentation tasks. Let us now illustrate their impact on the computation of the label maps. For this purpose we use synthetic Green Field data-set, with 3 classes, described by two features. If we quantize all the features by 8 bit, we can map the whole data set to the 2-dimensional 256 x 256 feature space. If we accumulate the sample points in such representation, it will correspond to the probability densities. For the visualization we will mark these densities, belonging to different classes, with tree different colors: red, green and blue (see Figure below).
- The original distributions of 160'000 samples from the dataset
- Naïve Bayes model
- Gaussian Model: the distribution is approximated with a single Gaussian per class
- Sequential Gaussian Mixture Model
- Gaussian Mixture Model, estimated with help of Expectation-Maximization algorithm
- k-Nearest Neighbors classifier
- Support Vector Machines classifier
- Random Forest classifier
- Artificial Neural Networks classifier
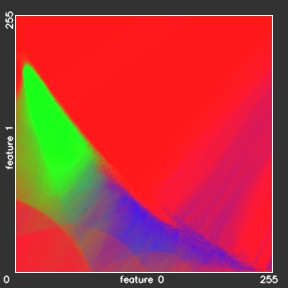
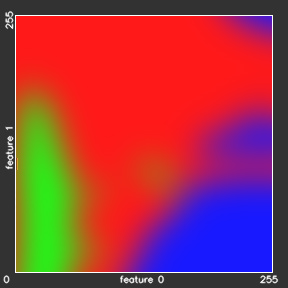
As we can observe from the Figure above, the generative models (Bayes and Gaussian mixtures) try to reproduce the original distributions. In order to do this precisely, a methods need to remember all the samples from the Green Field dataset – 160\’000 parameters. Or, in general, restricting ourself to the 8-bit features, a method needs to remember k·256^m values, where k is the number of categories and m is the number of features. The main idea of the generative models is to rebuild the original distribution using much less parameters and therefore generalize the model for samples, that were not observed during training. Bayes model approximates the distribution using only k·256·m parameters, and the Gaussian mixture model — k·G·m·(m +1) parameters, where G is the number of Gaussians in the mixture.
As opposed to the generative models, the discriminative models (Neural Networks, Random Forests, Support Vector Machines and k-Nearest neighbors) do not approximate the original distributions, but provide direct predictions for all testing samples. This grants the discriminative models more generalization power: In the areas, where hardly any training sample was met (left bottom and right top corners of the initial distribution image on Figure) all the generative models show black areas with almost zero potentials, while all the discriminative models how a high confidence about the class labels for these areas.